一、X 质数
题目
题目链接:0X质数 - 蓝桥云课
问题描述
对于一个含有 M 个数位的正整数 N ,任意选中其中 K 个不同的数位(0≤K<M),将这些选中的数位删除之后,余下的数位按照原来的顺序组成了一个新的数字 P 。如果至少存在一个 P 是质数,我们就称 N 是一个 X 质数。例如,对于整数 7869 ,我们可以删去 7 和 6 ,得到一个新的数字 89 ,由于 89 是一个质数,因此 7869 是一个 X 质数。又如,对于整数 77 ,可以删去一个 7 后变为质数 7 ,因此 77 也是一个 X 质数。
请问 1 (含)至 1000000(含)中一共有多少个不同的 X 质数。
解析
先通过埃氏筛,获取到范围内的所有质数。然后遍历每个数字的所有子串,查看是否满足 X 质数的定义,我们只要找到一个符合条件的子串即可退出循环,只要子串是质数或者 X 质数,我们都可以认定当前数字为 X 质数。
这里在寻找每个数的子串的时候,可以采用二进制的方式,详情查看:通过位运算快速生成所有的子序列|祀梦的个人博客
答案
# import os
# import sys
# def is_prime(n):
# _nums = [True] * (n + 1)
# _nums[0] = _nums[1] = False
# for i in range(2, n):
# if _nums[i]:
# for j in range(i ** 2, n + 1, i):
# _nums[j] = False
# return _nums
# N = 1000000
# nums = is_prime(N)
# ans = 0
# for num in range(N + 1):
# digits = [int(n) for n in str(num)]
# length = len(str(num))
# for mask in range(1,1 << length):
# subseq = 0
# for i in range(length):
# if mask & ( 1 << i ):
# subseq = subseq * 10 + digits[i]
# if nums[subseq]:
# nums[num] = True
# ans += 1
# break
# print(ans) # 989457
print(989457)二、顶板上的正方形
题目
题目链接:0钉板上的正方形 - 蓝桥云课
问题描述
小蓝有一个大小为 10×1010×10 钉板,如下图所示,上面等距分布着 10×1010×10 个钉槽(上下/左右相邻的钉槽之间的距离均相同)。其中有一些钉槽上面有钉子, 在图中用红色来进行标注,白色则表示此处没有钉子。小蓝喜欢用橡皮筋在钉 子上围出正方形图案,即选择钉板上的四个钉子,将其作为正方形的四个顶点, 从而把橡皮筋拉伸为一个正方形。
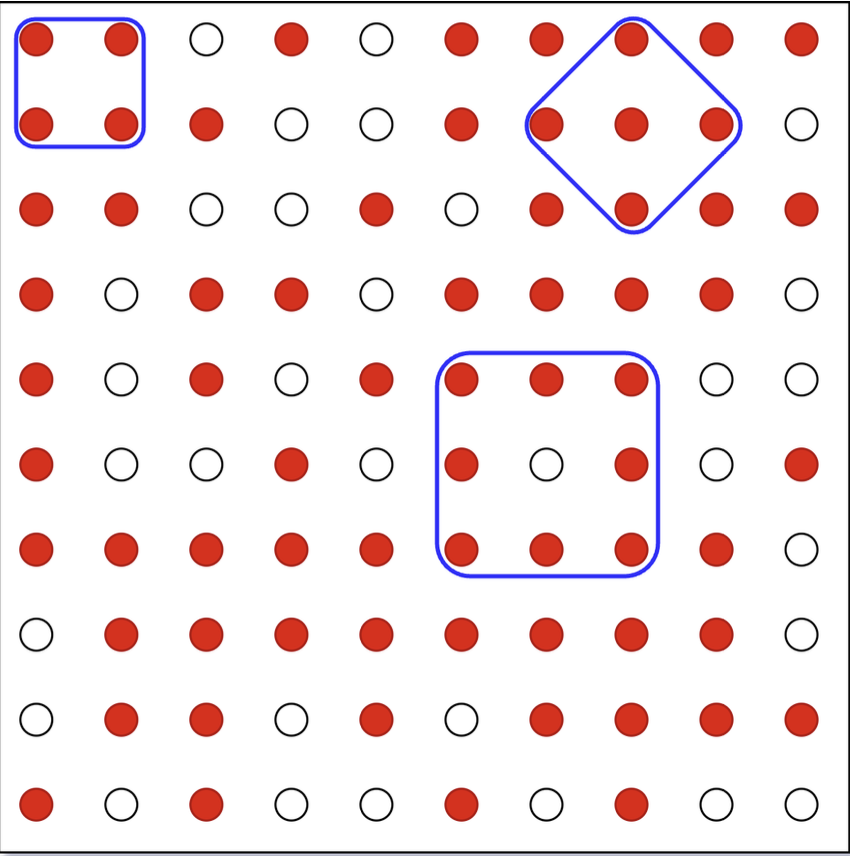
现在,小蓝想要知道在这个钉板上,可以围出多少种边长不同的正方 形?(相同边长的正方形均视作是同一种,不用考虑正方形的位置)。图中展示 了三种不同边长的正方形,其中蓝色线条表示橡皮筋。
解析
参考了评论区的大哥(马国良的个人主页 - 蓝桥云课)的思路,如下图所示
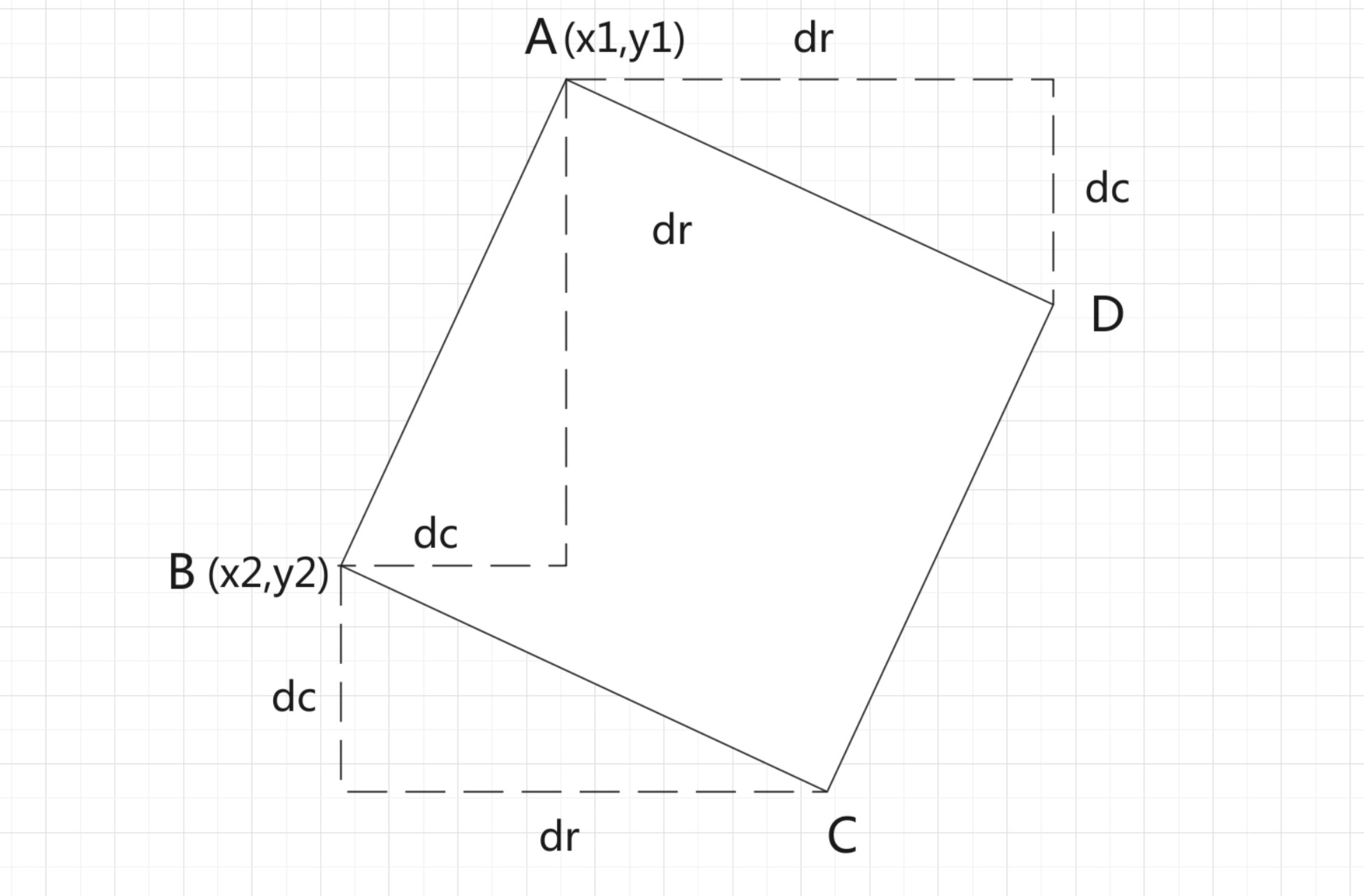
dr 为行之间的差距
dc 为列之间的差距
我们遍历 A 和 B,计算 C 和 D 的坐标,分别为 ( x2 + dr , y2 - dc ),( x1 + dr , y1 - dc )
然后确保CD没有超过棋盘范围并且都有钉子即可
答案
import os
import sys
from itertools import combinations
arr = [
[1, 1, 0, 1, 0, 1, 1, 1, 1, 1],
[1, 1, 1, 0, 0, 1, 1, 1, 1, 0],
[1, 1, 0, 0, 1, 0, 1, 1, 1, 1],
[1, 0, 1, 1, 0, 1, 1, 1, 1, 0],
[1, 0, 1, 0, 1, 1, 1, 1, 0, 0],
[1, 0, 0, 1, 0, 1, 0, 1, 0, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
[0, 1, 1, 0, 1, 0, 1, 1, 1, 1],
[1, 0, 1, 0, 0, 1, 0, 1, 0, 0]
]
points = [(i, j) for i in range(10) for j in range(10) if arr[i][j]]
squares = set()
for (x1, y1), (x2, y2) in combinations(points, 2):
dx, dy = x1 - x2, y1 - y2
x3 = x2 + dy
y3 = y2 - dx
x4 = x1 + dy
y4 = y1 - dx
if all(0 <= coord < 10 for coord in [x3, y3, x4, y4]):
if arr[x3][y3] and arr[x4][y4]:
squares.add(dx*dx + dy*dy)
print(len(squares))三、整数变换
题目
题目链接:0整数变换 - 蓝桥云课
问题描述
小蓝有一个整数 n。每分钟,小蓝的数都会发生变化,变为上一分钟的数减去上一分钟的数的各个数位和。
例如,如果小蓝开始时的数为 23,则下一分钟变为 23−(2+3)=18,再下一分钟变为 18−(1+8)=9,再下一分钟变为 9−9=0,共经过了 3 分钟变为 0。
给定一个正整数,请问这个数多少分钟后变为 0。
解析
这题直接暴力就过了。
Python3 跑出来只能通过 60% 的测试用例,用 PyPy3 就好了。
答案
import os
import sys
num = int(input())
count = 0
while num != 0:
num -= sum(map(int,str(num)))
count += 1
print(count)整数变换的第二种做法
答案
import os
import sys
# 对 1000 以内的数进行预处理
# difference[i][j] 代表每次减去 sum_digits(i) + j 之后,剩余的值,可能为负数
# step[i][j] 记录最终结果
# 题目中数字的最大值范围为 10的9 次方,我们每一步多减去的 j 值代表的其实是前六位的和
# j 最大也就是 54( 前六位都是9 )
difference = [[0 for _ in range(55)] for _ in range(1000)]
step = [[0 for _ in range(55)] for _ in range(1000)]
# 这里要考虑一下边界情况,有可能后三位为 0 前六位还有
# 这个时候要减去前六位的值
# 并且步数需要加一步
difference[0] = [-num for num in range(55)]
step[0] = [0] + [1 for num in range(54)]
# 先计算出 0 ~ 999 以内的数的值
for i in range(1,1000):
# 遍历所有可能的 j 值
for j in range(55):
ans,num = 0,i
while num > 0:
num -= ( sum(map(int,str(num))) + j )
ans += 1
difference[i][j] = num
step[i][j] = ans
# 当 num 小于 1000 的时候直接返回
num = int(input())
if num < 1000:
print(step[num][0])
else:
ans = 0
while num:
if num < 1000:
ans += step[num][0]
break
# x 为前六位
# y 为后三位
x = num // 1000
y = num % 1000
# 直接加上步数,以及溢出的值即可
ans += step[y][sum(map(int,str(x)))]
num = x * 1000 + difference[y][sum(map(int,str(x)))]
print(ans)四、火车运输
五、最大区间
题目
题目链接:0最大区间 - 蓝桥云课
问题描述
给定一个长度为 n 的序列 Ai,求 L,R 使 (R−L+1)⋅min(AL,AL+1,…,AR) 尽可能大,其中 min 表示最小值。
你只需要输出最大的值即可,不需要输出具体的 L,R。
解析
这道题要求给定字符串中的 (R−L+1)⋅min(AL,AL+1,…,AR) 的最大值,每次计算区间内的最小值再扩展区间很麻烦,我们可以转换一下思路以当前元素为区间内的最小元素,视为右边界,然后不断向左边扩展,一直到小于当前元素的位置停下,就可以得到当前区间的结果。(这里为什么不用向右边扩展,因为如果存在这种情况的话,右边向左扩展的时候会包括这一段)我们可以采用单调递增栈来加快寻找的速度,0 是为了确保清空栈。
可以用下面这个例子 debug 一下程序查看运行过程。
n = 6
A = [1,2,3,2,3,2]
(感觉解释的还是不太够清楚,有啥问题可以直接评论)
答案
import os
import sys
n = int(input())
A = list(map(int,input().split()))
A.append(0)
stack = []
ans = 0
for i in range(n+1):
while stack and A[i] <= A[stack[-1]]:
prev_i = stack.pop()
L = stack[-1] if stack else -1
ans = max( ( i - L - 1 ) * A[prev_i] ,ans)
stack.append(i)
print(ans)


